The Z distribution and t distribution are two of the most looked-for distributions in hypothesis testing as a part of inferential statistics. More often than not in Data Science, it is important for a data scientist to encounter situations or problem statements that require inferences to be made using a hypothesis to understand more about the data.
A small note on Inferential Statistics:
Descriptive Statistics helps you describe the data. Diagnostic statistics help you to dive deeper into your data. Inferential statistics helps you to take data from samples and make predictions (‘inferences’) from the data. In this, you take data from a sample and make generalizations about the entire population. Inferential statistics are generally used by researchers and scientists in the medical industry the most to make inferences about how medicines work.
In this article, we’ll go over both, i.e., the Z distribution and t distribution, to understand when in hypothesis testing should you choose a ‘Z’ distribution and when a ‘t’ distribution.
Feel free to skip to any section or particular distribution you want to know more about.
Also, read -> What is a virtual environment and how to use it in Python?
What are Z distribution and t distribution?
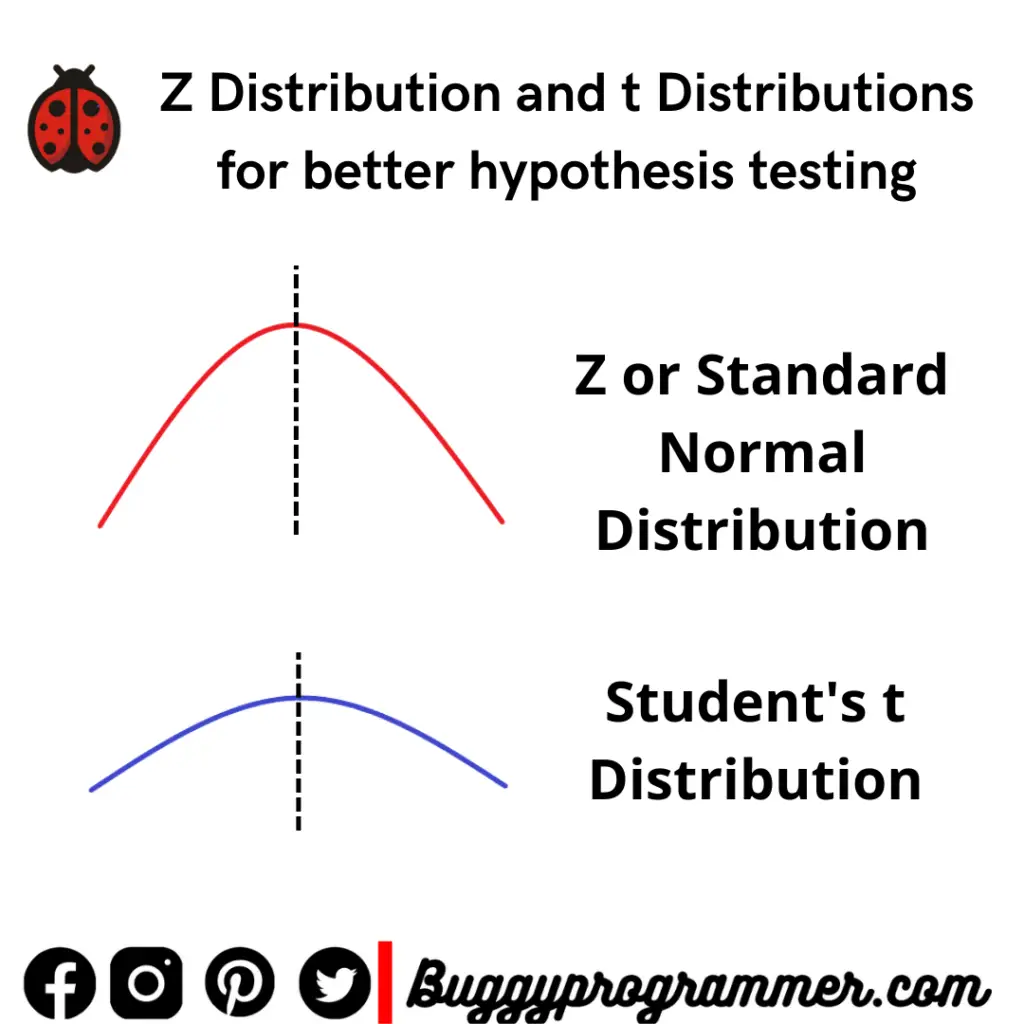
Z Distribution
A Z distribution is a special kind of Gaussian or Normal distribution and is also called the ‘standard’ normal distribution where the distribution has a mean of 0 and a standard deviation of 1.
It is one of the most widely used distributions in statistics, especially in inferential statistics because every distribution is estimated to represent a normal distribution (with a standard deviation and a centered mean) after taking enough samples of the data. The normal distribution is a simple bell-shaped curve that is stretched from the left to right centered about a mean and a standard deviation.
The difference between the Normal Distribution and Z distribution in inferential statistics is that the Normal distribution can have any kind of peak, and mean, and can have any standard deviation, whilst the standard normal distribution or the standard Gaussian distribution or the Z distribution, have a fixed mean and standard deviation of 0 and 1 respectively.
Read more about the Z Distribution here: Z Distribution
t Distribution
The t distribution, also known as the Student’s t distribution, after its founder, William Gosset whose pen name was Student, is from a family of distributions that represent the normal distribution closely and the only difference is that the peak is flatter and the tails of the distribution are longer.
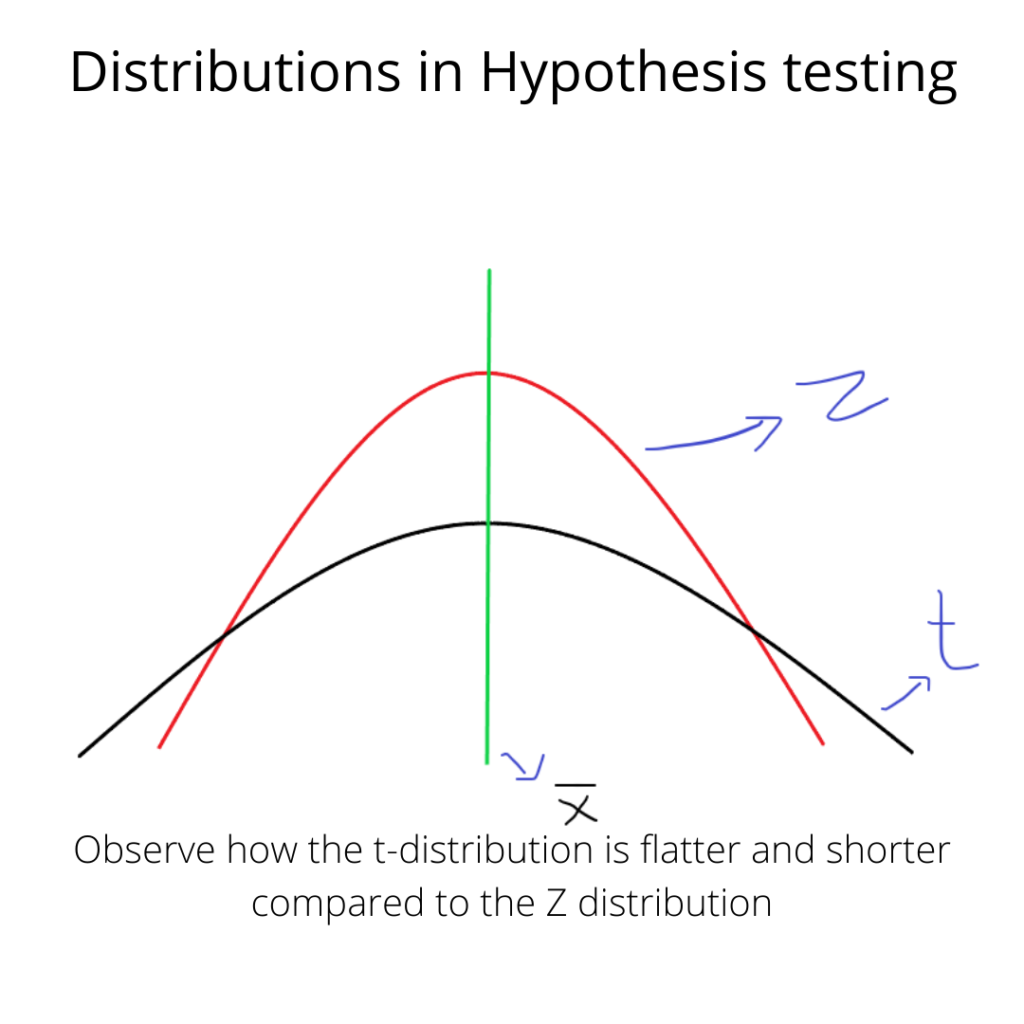
The larger the sample size of the student’s t distribution, the more it represents a normal distribution. The primary difference between Z distribution and t distribution is that the latter comes into the picture when the sample size is not large enough to represent a normal distribution.
The t distribution is the other most used distribution after the z distribution in a hypothesis test.
Read more about the t Distribution here: t Distribution
When to use the Z Distribution?
When can you use the Z test and what are the conditions to fulfill for a Z distribution to be used?
- A Random Sample
- All are observations in the data are independent
- A minimum of 30 observations in the sample for Standard Deviation
- The standard deviation is known.
Once you have all these checked, you can use a Z test, to find the test statistic, compare it to the values in the Z distribution or the Standard normal distribution and find the Z critical value to come to a conclusion in your hypothesis tests.
When to use the t Distribution?
The only time you need to shift from a Z distribution to a t distribution is when you need to use a sample size that is less than 30. For the smaller sample with no knowledge of the population standard variance, you can estimate the test statistic using a sample error where the standard deviation of the sample and the number of observations come into the picture.
The test statistic i.e., ‘t’ in this case can be used with a Student’s t distribution and the value can be compared with the critical ‘t’ value to arrive at the conclusion of the hypothesis test.
Is there a better distribution of the two?
Because the distributions are used in different scenarios and can help people in their hypothesis tests to get inferences from the data, you need to ensure that you choose the right distribution for the right sample of data.
Find out how to do a hypothesis test here: Hypothesis testing
If you apply a Z distribution and a Z test to a sample that is too small it won’t give you the right answers to your hypothesis.
So, there is no ‘better’ distribution of the two, only that the right distribution for the right situation will get you all you need to do.
Conclusion
Hypothesis tests are an important thing to learn in Data Science and are always good to learn if you are statistically inclined and want to go towards the research side of things in any industry. The Z distribution and t distribution are very useful for the same and in some cases, you might want to look for the chi-square distribution or the F distribution (which we will unravel in articles to come).
The entire concept of understanding how these distributions work will help you choose the right type of testing for your own research work and will help your stakeholders make the right decisions with inferential statistics in the picture. Making inferences from your data can be a difficult thing to do until you don’t use hypotheses or assumptions to confirm. However, by actually using Z distribution and t distribution, you can decide whether something in your data is required to be checked properly for any changes from the status quo.
Find out how to do a hypothesis test in Python using the following YouTube tutorial if you use Python: Hypothesis test in Python
For more such articles, check out our website -> Buggy Programmer
