It is very important to not just rely on a single metric to evaluate our machine learning model. Today we are going to discuss two such regression metrics, the difference between R-square vs standard error of estimate, and find out which can be a better option.
Let’s first start with understanding what these two metrics mean.
What is R-square?
R-square is a goodness of fit. It returns a value that shows how good is the Machine Learning model in prediction. In other words, It tells us how much of the variation is explained by our prediction model. It ranges from 0 to 1.
If the R-square value is 0.60 (60%), this means our model is explaining 60% of the variation in the data. But still, this value can be misleading, How? This we will understand further in this blog. The difference between R-square vs Standard error of estimate comes from also the possibility that you can be misled when you use R-square.
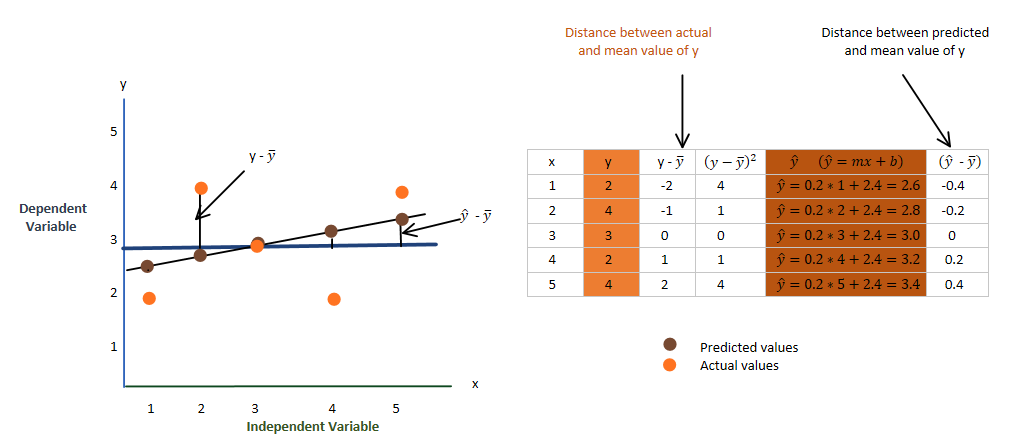
The mean of the y-axis ( ȳ )
I have already calculated the slope and bias so that I can manually calculate the predicted values and show them to you all using the table above. You don’t need to worry about how slope and bias were calculated, just keep reading and understanding this blog.
The equation for the line is,
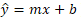
where y-cap is our predicted values
As I said above, in R2, we are comparing the distance between actual values and the mean of the y-axis with the distance between the predicted value and the mean of the y-axis. Let’s, discuss its formula,
The formula for R2,
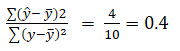
R2 = 0.4, which is by the way bad and it says that it is able to explain only 40% of the variation in data. In such a case, you need to work on your Machine Learning model to make it better. Here we go with understanding the Standard error of estimate which will clearly show you why there is a Difference between R-square vs Standard error of estimate.
What is the Standard Error of Estimate?
The standard error is the difference between the actual and predicted values.
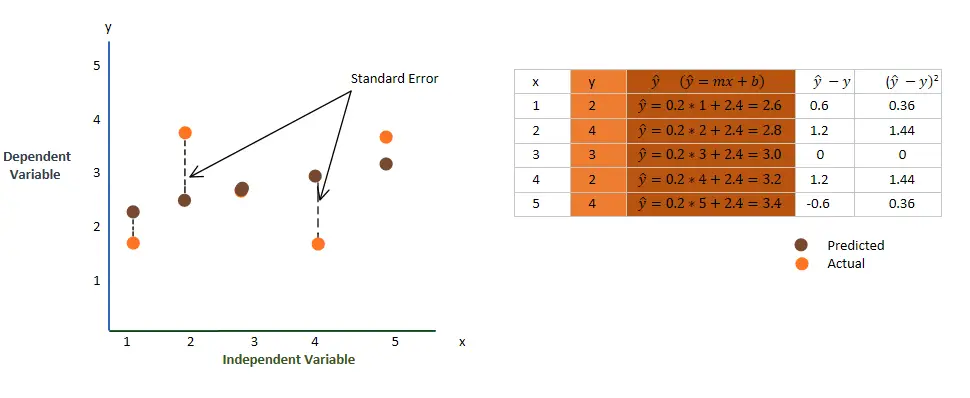
The formula for Standard Error of Estimate,
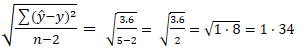
The standard error value near zero is better, which means that the distance between the actual and predicted value is lesser and hence our prediction is closer to the actual output. That’s it for Standard error.
What is the Difference between R-square vs Standard error of estimate?
Consider below given two graphs
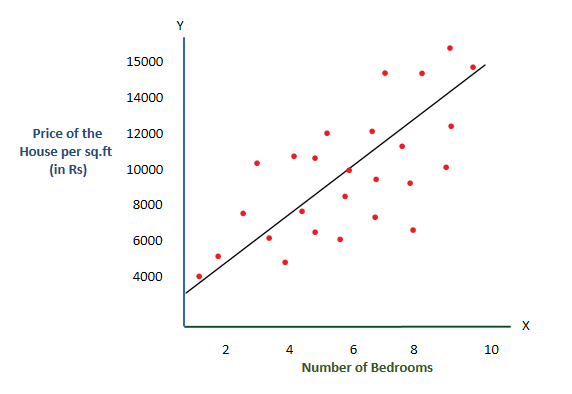
Simply to understand, let’s consider, I have calculated the R2 and Standard error and given in below table
| R square | 0.72 |
| Standard Error | 5.75 |
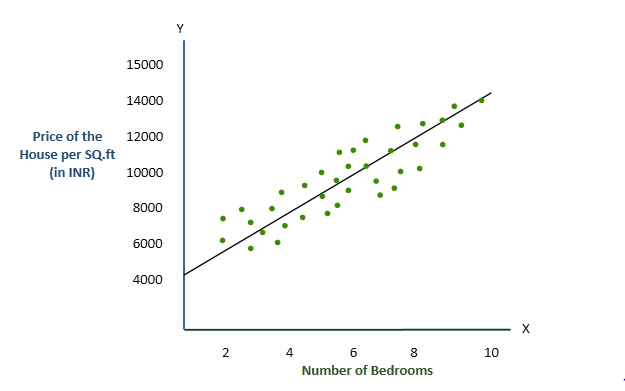
Now consider this second graph, I have calculated its R2 value and Standard error and it resulted in the below values.
| R-square | 0.72 |
| Standard Error | 1.24 |
It is very much possible that the R-square value remains the same or has a very slight improvement but the prediction has been improved. This improvement was missed by the R2 calculation but has been explained by the Standard error.
So now you understand why the Standard error value can be better than R2 in some cases. In case you want to know more about the difference between R-square vs Standard error of estimate;
Here are Some Links for your reference:
https://en.wikipedia.org/wiki/Coefficient_of_determination
Youtube Video by StatQuest:
https://www.youtube.com/watch?v=2AQKmw14mHM
For more such content, check out our website -> Buggy Programmer

Data Scientist with 3+ years of experience in building data-intensive applications in diverse industries. Proficient in predictive modeling, computer vision, natural language processing, data visualization etc. Aside from being a data scientist, I am also a blogger and photographer.
- Aman Kumarhttps://buggyprogrammer.com/author/buggy5454/
- Aman Kumarhttps://buggyprogrammer.com/author/buggy5454/
- Aman Kumarhttps://buggyprogrammer.com/author/buggy5454/
- Aman Kumarhttps://buggyprogrammer.com/author/buggy5454/





